Sitemap
A list of all the posts and pages found on the site. For you robots out there is an XML version available for digesting as well.
Pages
Posts
Future Blog Post
Published:
This post will show up by default. To disable scheduling of future posts, edit config.yml and set future: false.
Blog Post number 4
Published:
This is a sample blog post. Lorem ipsum I can’t remember the rest of lorem ipsum and don’t have an internet connection right now. Testing testing testing this blog post. Blog posts are cool.
Blog Post number 3
Published:
This is a sample blog post. Lorem ipsum I can’t remember the rest of lorem ipsum and don’t have an internet connection right now. Testing testing testing this blog post. Blog posts are cool.
Blog Post number 2
Published:
This is a sample blog post. Lorem ipsum I can’t remember the rest of lorem ipsum and don’t have an internet connection right now. Testing testing testing this blog post. Blog posts are cool.
Blog Post number 1
Published:
This is a sample blog post. Lorem ipsum I can’t remember the rest of lorem ipsum and don’t have an internet connection right now. Testing testing testing this blog post. Blog posts are cool.
projects
Mode localization in weakly coupled microelectromechanical resonators
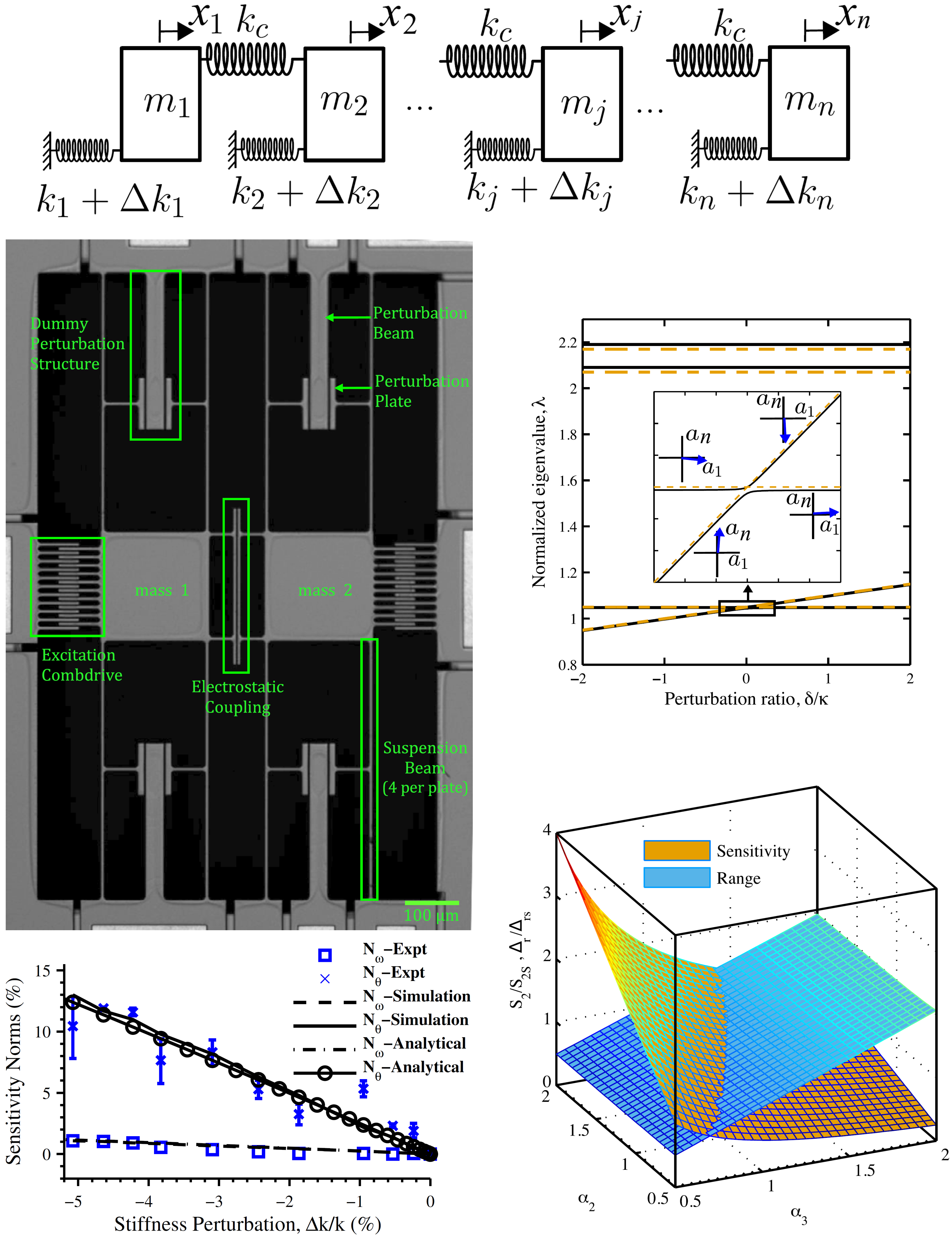 Weakly coupled, symmetric resonator systems exhibit the phenomena of eigenvalue veering and associated mode localization induced by symmetry breaking parametric changes in the system. This results in orders of magnitude higher sensitivity of mode shapes compared to the sensitivity of resonant frequencies of such systems. Also, their sensitivity varies inversely with the strength of coupling. This opens an alternative sensing paradigm based on mode shapes instead of resonant frequencies. We develop theoretical analysis of mode localization in weakly coupled resonators and validate the results by characterizing purposely designed microelectromechanical (MEMS) devices.
Weakly coupled, symmetric resonator systems exhibit the phenomena of eigenvalue veering and associated mode localization induced by symmetry breaking parametric changes in the system. This results in orders of magnitude higher sensitivity of mode shapes compared to the sensitivity of resonant frequencies of such systems. Also, their sensitivity varies inversely with the strength of coupling. This opens an alternative sensing paradigm based on mode shapes instead of resonant frequencies. We develop theoretical analysis of mode localization in weakly coupled resonators and validate the results by characterizing purposely designed microelectromechanical (MEMS) devices.
[1] Manav, M., Reynen, G., Sharma, M., Cretu, E., & Phani, A. S. (2014). Ultrasensitive resonant MEMS transducers with tuneable coupling. Journal of Micromechanics and Microengineering, 24(5), 055005.
[2] Manav, M., Phani, A. S., & Cretu, E. (2017). Mode localized MEMS transducers with voltage-controlled linear coupling. Journal of Micromechanics and Microengineering, 27(5), 055010.
[3] Manav, M., Phani, A. S., & Cretu, E. (2018). Mode localization and sensitivity in weakly coupled resonators. IEEE Sensors Journal, 19(8), 2999-3007.
Mechanics of a polymer brush
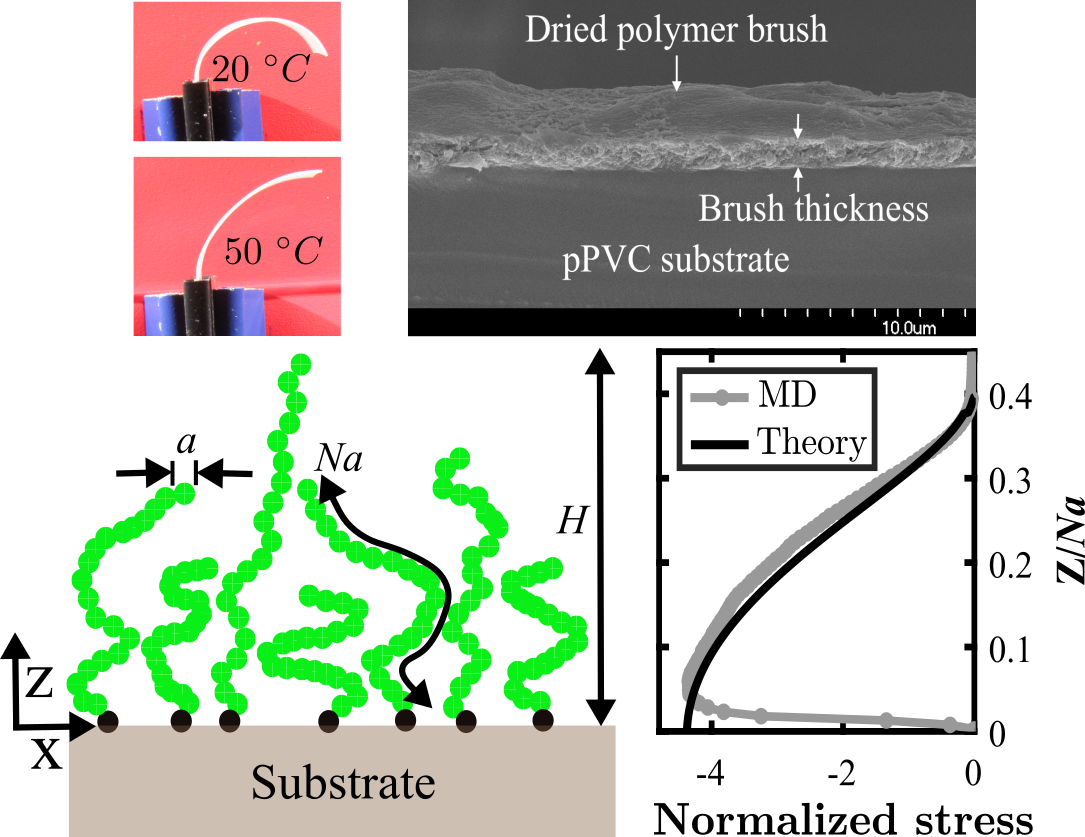 Polymer brushes are soft active materials which form from dense tethering of polymer chains on a substrate. They provide a facile means of converting chemical energy into mechanical work at nanoscale, achieved through stimuli-induced conformation changes. Our research constituted pioneering work on the stress within a polymer brush. Our theoretical and computational work combined polymer physics theories with continuum mechanics to predict stress in a brush and its stimuli-response, and validated the results using molecular dynamics (MD) simulation. Our research has significant implications in the design of brush based nanoactuators and self-folding of 2D materials to generate 3D structures using brushes, and can contribute to our understanding of the bending of a biological membranes due to the disordered proteins on their surface.
Polymer brushes are soft active materials which form from dense tethering of polymer chains on a substrate. They provide a facile means of converting chemical energy into mechanical work at nanoscale, achieved through stimuli-induced conformation changes. Our research constituted pioneering work on the stress within a polymer brush. Our theoretical and computational work combined polymer physics theories with continuum mechanics to predict stress in a brush and its stimuli-response, and validated the results using molecular dynamics (MD) simulation. Our research has significant implications in the design of brush based nanoactuators and self-folding of 2D materials to generate 3D structures using brushes, and can contribute to our understanding of the bending of a biological membranes due to the disordered proteins on their surface.
[1] Manav, M., Anilkumar, P., & Phani, A. S. (2018). Mechanics of polymer brush based soft active materials–theory and experiments. Journal of the Mechanics and Physics of Solids, 121, 296-312.
[2] Manav, M., Ponga, M., & Phani, A. S. (2019). Stress in a polymer brush. Journal of the Mechanics and Physics of Solids, 127, 125-150.
[3] Manav, M., Ponga, M., & Phani, A. S. (2020). Stress in a stimuli-responsive polymer brush. Macromolecules, 54(1), 170-182.
Unlocking of the unexpected behaviors of polyurea
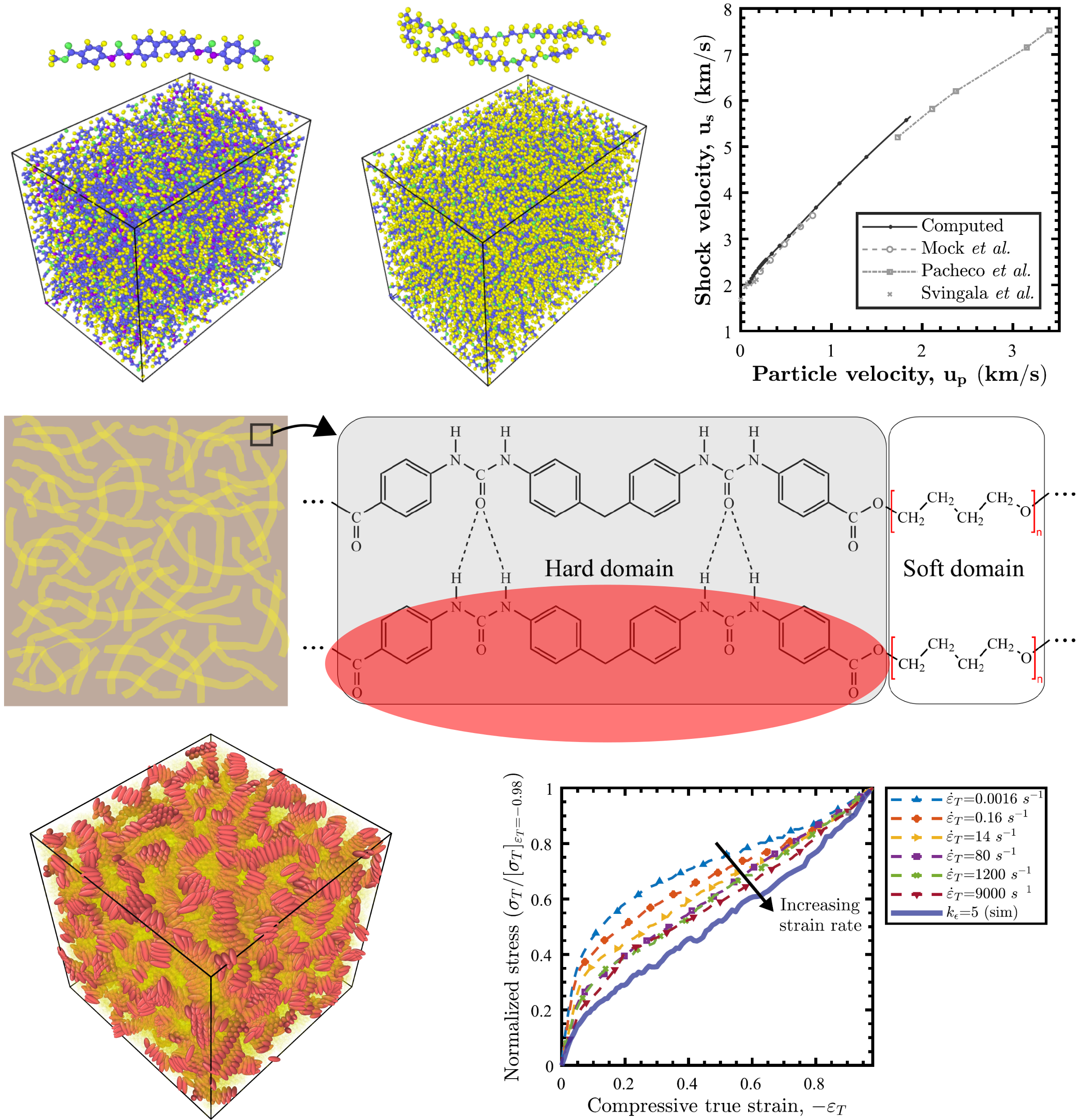 Polyurea is a thermoplastic elastomer with excellent shock and impact resistance. At high strain rates (~ 10^6 s^-1) and pressures (~ 9 GPa), its shear modulus (500 MPa) matches the shear modulus of high strength steels. Molecular dynamics (MD) simulation can shed light on the molecular origins of this response. However, MD simulation of polyurea is challenging due to its phase-segregated microstructure and the presence of a wide range of associated length and time scales. Our work instead leverages the microstructure to perform multiscale shock simulation of the domains in polyurea and yielded insights into the molecular-scale mechanisms underpinning shock mitigation. To develop a comprehensive understanding of the microstructural mechanisms at play, we have also developed a novel generic coarse-grained model of polyurea as a liquid-crystalline polymer.
Polyurea is a thermoplastic elastomer with excellent shock and impact resistance. At high strain rates (~ 10^6 s^-1) and pressures (~ 9 GPa), its shear modulus (500 MPa) matches the shear modulus of high strength steels. Molecular dynamics (MD) simulation can shed light on the molecular origins of this response. However, MD simulation of polyurea is challenging due to its phase-segregated microstructure and the presence of a wide range of associated length and time scales. Our work instead leverages the microstructure to perform multiscale shock simulation of the domains in polyurea and yielded insights into the molecular-scale mechanisms underpinning shock mitigation. To develop a comprehensive understanding of the microstructural mechanisms at play, we have also developed a novel generic coarse-grained model of polyurea as a liquid-crystalline polymer.
[1] Manav, M., & Ortiz, M. (2021). Molecular dynamics study of the shock response of polyurea. Polymer, 212, 123109.
[2] Manav, M., Ponga, M., & Ortiz, M. (2023). Modeling hard–soft block copolymers as a liquid crystalline polymer. Polymer, 287, 126389.
[3] Manav, M., Ponga, M., & Ortiz, M. Dynamic response of a hard-soft block copolymer modeled as a liquid crystalline polymer. In preparation.
Implicit neural representation for 3D printing process optimization
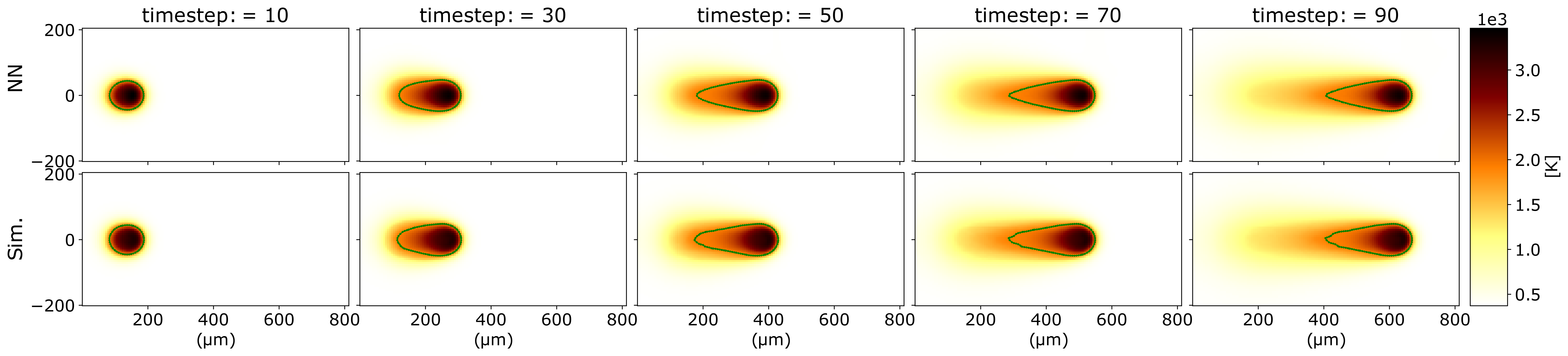 Laser powder bed fusion process (LPBF) promises to automate the fabrication of high quality custom designed metal parts. In LPBF, part fabrication progresses through sequential spreading of powder layers and their selective melting via a laser, leading to the formation of a melt pool, and subsequent solidification. The process has a large number of control parameters. However, the relationship between the process parameters and the quality of the fabricated part is complex. Disentangling it requires one to solve multiscale multiphysics problems which are computationally very expensive, precluding the application of this approach to process optimization and control. During the printing process, the temperature field, its gradient and cooling rate at the melt pool boundary, the geometry of the melt pool, among others, have a significant effect on the microstructure of the fabricated part and residual stresses in the parts, and consequently on the part properties. Hence, obtaining the relation between these quantities and the process parameters and their fast inference is imperative to optimizing the printing process. We propose a data-driven, differentiable neural network model designed to learn the temperature field, its gradient, and the cooling rate, while implicitly representing the melt pool boundary as a level set in laser powder bed fusion. The implicit neural representation of the melt pool boundary as a level set also enables the inference of the solidification rate and the rate of change in melt pool geometry relative to process parameters.
Laser powder bed fusion process (LPBF) promises to automate the fabrication of high quality custom designed metal parts. In LPBF, part fabrication progresses through sequential spreading of powder layers and their selective melting via a laser, leading to the formation of a melt pool, and subsequent solidification. The process has a large number of control parameters. However, the relationship between the process parameters and the quality of the fabricated part is complex. Disentangling it requires one to solve multiscale multiphysics problems which are computationally very expensive, precluding the application of this approach to process optimization and control. During the printing process, the temperature field, its gradient and cooling rate at the melt pool boundary, the geometry of the melt pool, among others, have a significant effect on the microstructure of the fabricated part and residual stresses in the parts, and consequently on the part properties. Hence, obtaining the relation between these quantities and the process parameters and their fast inference is imperative to optimizing the printing process. We propose a data-driven, differentiable neural network model designed to learn the temperature field, its gradient, and the cooling rate, while implicitly representing the melt pool boundary as a level set in laser powder bed fusion. The implicit neural representation of the melt pool boundary as a level set also enables the inference of the solidification rate and the rate of change in melt pool geometry relative to process parameters.
[1] Manav, M., Perraudin, N., Lin, Y., Afrasiabi, M., Perez-Cruz, F., Bambach, M., & De Lorenzis, L. (2024). MeltpoolINR: Predicting temperature field, melt pool geometry, and their rate of change in laser powder bed fusion. arXiv preprint arXiv:2411.18048.
Fracture mechanics with physics-informed AI
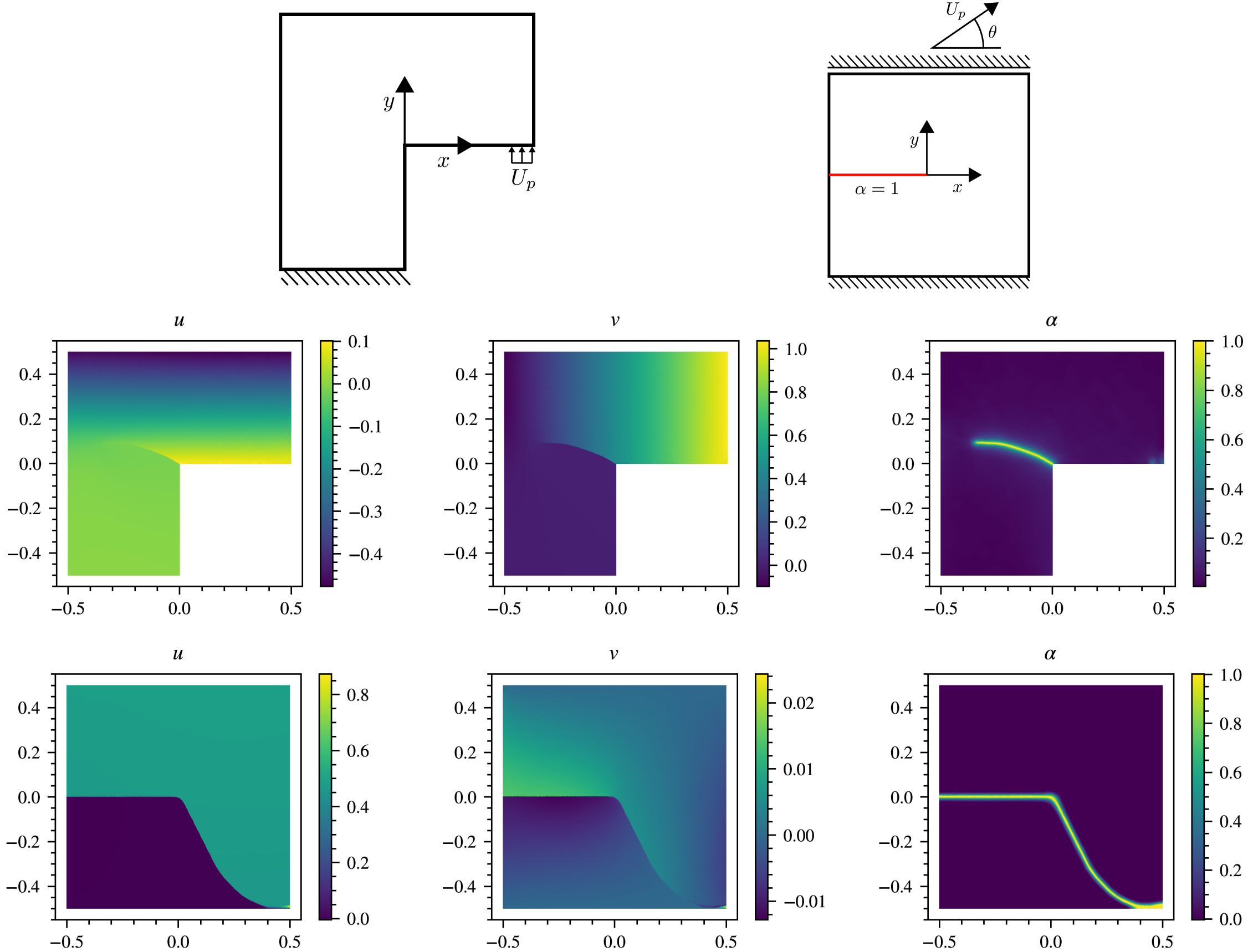 Phase-field modeling of fracture is a prominent fracture modeling approach which recasts the problem as a variational problem and promises to completely determine various complex fracture processes including crack nucleation, propagation, bifurcation, and coalescence, obviating the need for ad-hoc conditions. In this approach, a phase field is introduced which regularizes a crack. It is, however, a nonlocal model which introduces a small length scale. Resolving this length scale in computation is expensive. Hence, uncertainty quantification, design optimization, material parameter identification, among others, using this approach become prohibitively expensive. Deep learning offers a potential pathway to address this challenge. We explore the application of physics-informed neural networks (PINNs) and DeepONet (an operator learning framework) to phase-field fracture modeling with the aim to capture diverse fracture processes. The nonconvexity of the energy functional, and the initiation and evolution of the fields with sharp gradients governed by this energy are the two key challenges to learning the solution field. Guided by the challenges, we design a network, construct a loss function, and select an optimization scheme to learn the solution accurately. By solving some benchmark problems in the phase-field fracture literature, we exhibit the capability of the approaches to capture crack nucleation, propagation, kinking, branching and coalescence.
Phase-field modeling of fracture is a prominent fracture modeling approach which recasts the problem as a variational problem and promises to completely determine various complex fracture processes including crack nucleation, propagation, bifurcation, and coalescence, obviating the need for ad-hoc conditions. In this approach, a phase field is introduced which regularizes a crack. It is, however, a nonlocal model which introduces a small length scale. Resolving this length scale in computation is expensive. Hence, uncertainty quantification, design optimization, material parameter identification, among others, using this approach become prohibitively expensive. Deep learning offers a potential pathway to address this challenge. We explore the application of physics-informed neural networks (PINNs) and DeepONet (an operator learning framework) to phase-field fracture modeling with the aim to capture diverse fracture processes. The nonconvexity of the energy functional, and the initiation and evolution of the fields with sharp gradients governed by this energy are the two key challenges to learning the solution field. Guided by the challenges, we design a network, construct a loss function, and select an optimization scheme to learn the solution accurately. By solving some benchmark problems in the phase-field fracture literature, we exhibit the capability of the approaches to capture crack nucleation, propagation, kinking, branching and coalescence.
[1] Manav, M., Molinaro, R., Mishra, S., & De Lorenzis, L. (2024). Phase-field modeling of fracture with physics-informed deep learning. Computer Methods in Applied Mechanics and Engineering, 429, 117104.
[2] Kiyani, E., Manav, M., Kadivar, N., De Lorenzis, L., & Karniadakis, G. (2025). Predicting crack nucleation and propagation in brittle materials using deep operator networks with diverse trunk architectures. arXiv preprint arXiv:2501.00016.
Visualizing energy landscape in phase-field fracture using deep learning
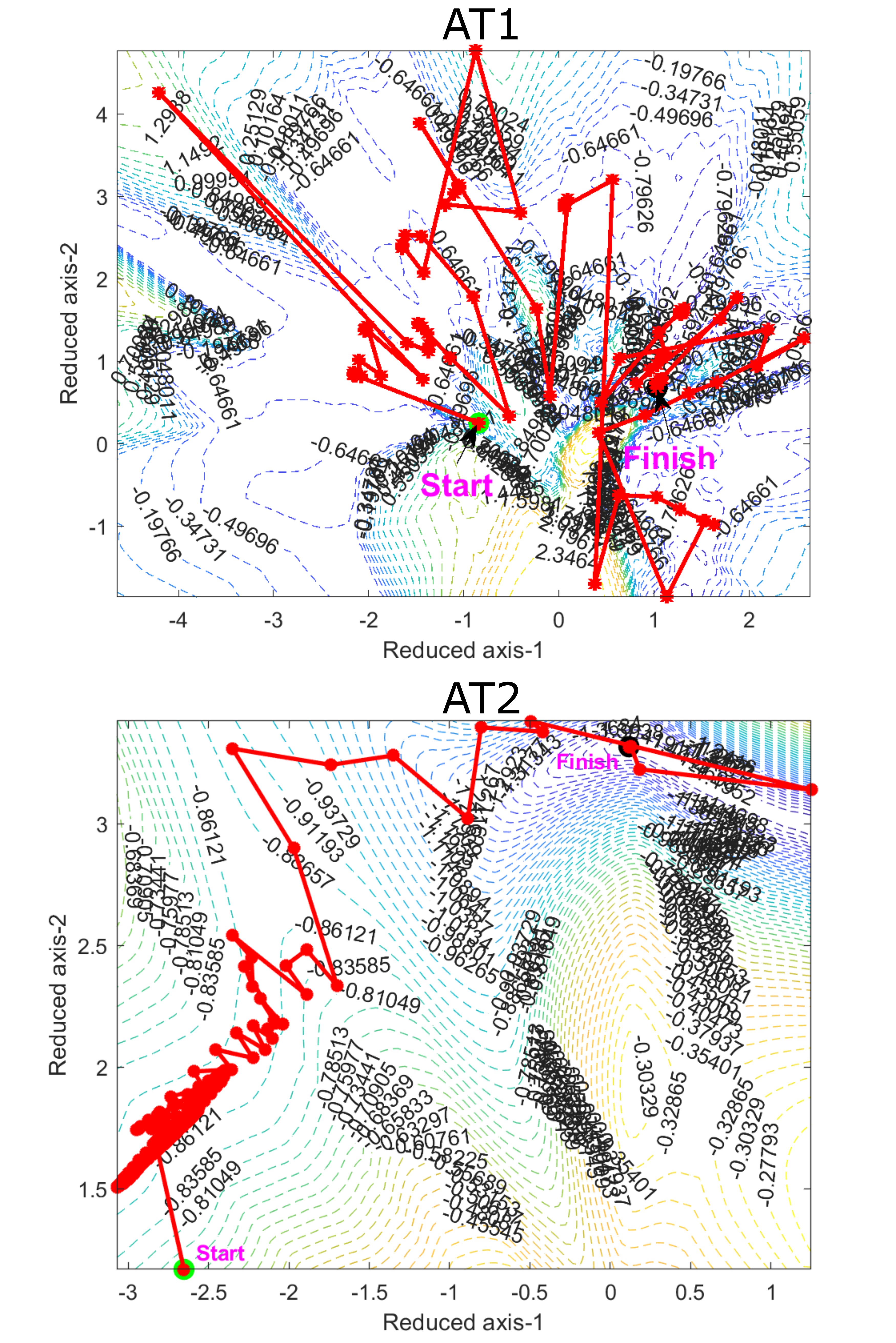 The energy landscape governs the dynamics of how a solution (energy minimum) is reached. Visualizing the energy landscape helps develop intuition about its critical features and low-dimensional structure. Additionally, it can guide the selection and design of solution algorithms. However, the solution field, even in a discrete setting, is high-dimensional. By applying linear and nonlinear order reduction techniques, we reduce the dimensionality to two, allowing for visualization of the solution approach. The plots on the left illustrate the differences between the features of the AT1 and AT2 model landscapes, and the solution trajectories at the loading stage where the phase field localizes in a 1D bar.
The energy landscape governs the dynamics of how a solution (energy minimum) is reached. Visualizing the energy landscape helps develop intuition about its critical features and low-dimensional structure. Additionally, it can guide the selection and design of solution algorithms. However, the solution field, even in a discrete setting, is high-dimensional. By applying linear and nonlinear order reduction techniques, we reduce the dimensionality to two, allowing for visualization of the solution approach. The plots on the left illustrate the differences between the features of the AT1 and AT2 model landscapes, and the solution trajectories at the loading stage where the phase field localizes in a 1D bar.
[1] Manav, M., & De Lorenzis, L. Visualization and characterization of energy landscape in phase-field fracture. In preparation.
publications
teaching
Mechanical Vibrations
Teaching assistant, UBC, 2013
Mechanics of Materials
Teaching assistant, UBC, 2015
Mechanical Engineering Laboratories
Teaching assistant, UBC, 2017
Mechanical Design
Teaching assistant, UBC, 2017
